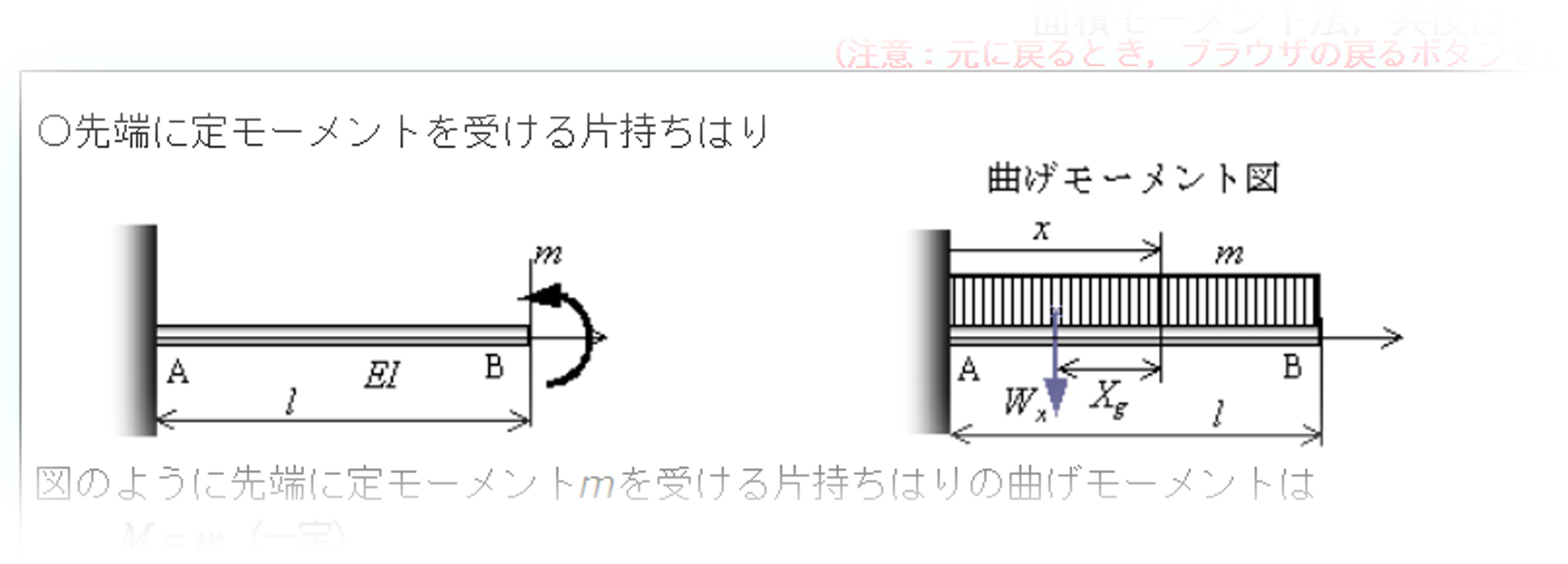
荷重qが作用する時の曲げモーメント図は、荷重pが作用する時の曲げモーメント図と同様です。 柱cd間は、c点に固定支点があると考えてください 。そうすると片持ち梁と同じ曲げモーメント図になります。 梁bc間は、曲げモーメント図が一定になります 。ここでも荷重qの作用線（力の方向に引く線）を書きましょう。するとキョリがlで一定となります。力はq. ⑶ 曲げモーメント（m） mc は 上側凸 なお、a点の曲げモーメントも自由端から 計算して、 ma したがって、荷重p が作用する片持ち梁の自由端からの距 離x の点の曲げモーメントはpx となり、荷重点からの垂直距 離（スパンの長さ）に比例して大きくなる。
梁の公式 荷重・形状 条件 曲げモーメント m反力 r･せん断力 q･全荷重 w たわみ δ p l rb a b w＝p rb＝p qb＝－p mb＝－pl pl3 δa＝ 3ei l rb a b p1 p2 abrb＝p1＋p2 qb＝－（p1＋p2） w＝p1＋p2 mb＝－（p1l＋p2b） 2 δa＝ ＋ 3ei p1l3 6ei p2b （3l－b） l rb a b ab p w＝p rb＝p
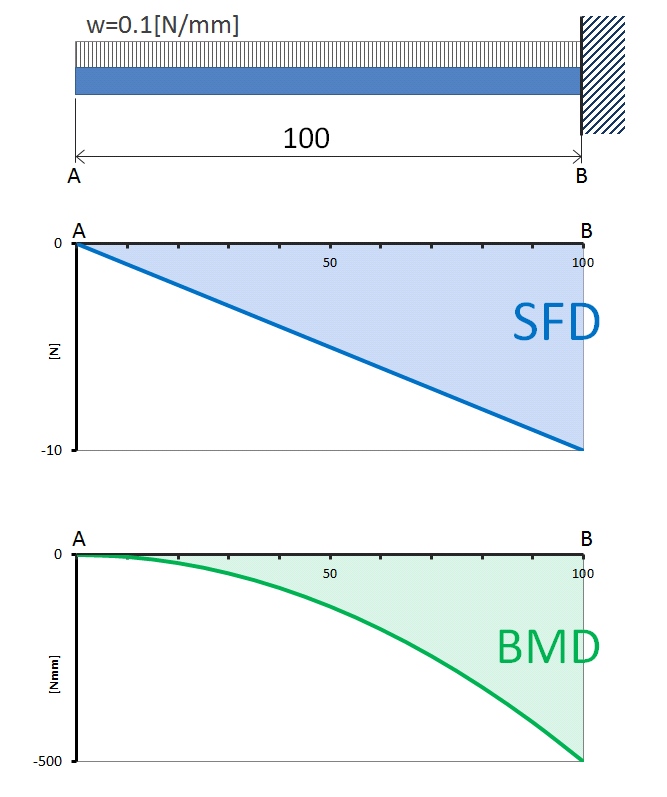
片 持ち 梁 曲げ モーメント 図. 次に、曲げモーメント図を描いていきます。 曲げモーメントは端部で支点反力と同じ値だけ発生します。そして、片持ち梁の自由端は 鉛直方向も水平方向も回転も全く固定しません 。 そのため、自由端では曲げモーメントは0knと言うことになります。 一端を固定し他端に横荷重 pを採用する梁のことを 片持ち梁 といい1点に集中して作用する荷重のことを 集中荷重 という。. 片持ち梁の曲げモーメント図 | 図, 関係, 分布.
L：荷重図 q：せん力図 m：曲げモーメント図 w：全荷重 m：曲げモーメント r：反力 θ：回転角 q：せん断力 δ：たわみ: 写真の赤い点線で示したのは、モーメント荷重を加えた際の 梁の変形を表していますが、 ①図のような片持ち梁では、全長にわたり下（又は上）が引張側になります。 モーメント荷重mと、固定端の反力モーメントm´は同じ大きさで、回転方向は逆になります。 ところが、 ②図のような場合では、ピン端の方は上が引張、固定端の方は下が引張側 というよう. 単純梁 ← 図をクリックすると、 各種計算式が表示されます。 反力、せん断、曲げモーメント、 たわみ、・・・.
片 持ち 梁 モーメント 図
【ほとんどのダウンロード】 片 持ち 梁 振動
【パワーメーター】ペダル水平分力を得る＜中華ゲージ追加＞ 信州MAKERS
等 分布 荷重 片 持ち 梁
片 持ち 梁 分布 荷重
【6分力計2018】TS2構想設計＜厚くなった＞ 信州MAKERS
