図5 最密充填球内をブラウン運動する分散粒子 分の溶液はaとbと の成分の二相に分離している.これ 図6 a ポリマー, b ポリマー, s 溶剤3 成分混合系の 相図2) 図7 2段階相分離の混合状態模式図 図8 典型的な海島二相組織 ( 39 ) 795 図1.5 1成分系と2 成分系の異相平衡の条件:(a) 1 成分系(a 元素)ではi 相とii 相の自由エ ネルギー(gi a, g ii a)の交点が平衡温度,(b) 2 成分系(a 元素とb 元素)では, 相と 相の組成 -自由エネルギー(g ,g )の共通接点①②が平衡組成.
種類の成分 (j=1,2,…, q ), n 個の相 (i=1,2,…, n ) 例)1成分系( q 1 )では, 2相共存( n2 )は,共存線( f 1 ), 3相共存( n 3 )は,三重点( f 0 )となる。 以下では,多成分系の相図について説明する。ギブズの相律より成分数の増加と共に共存境界.
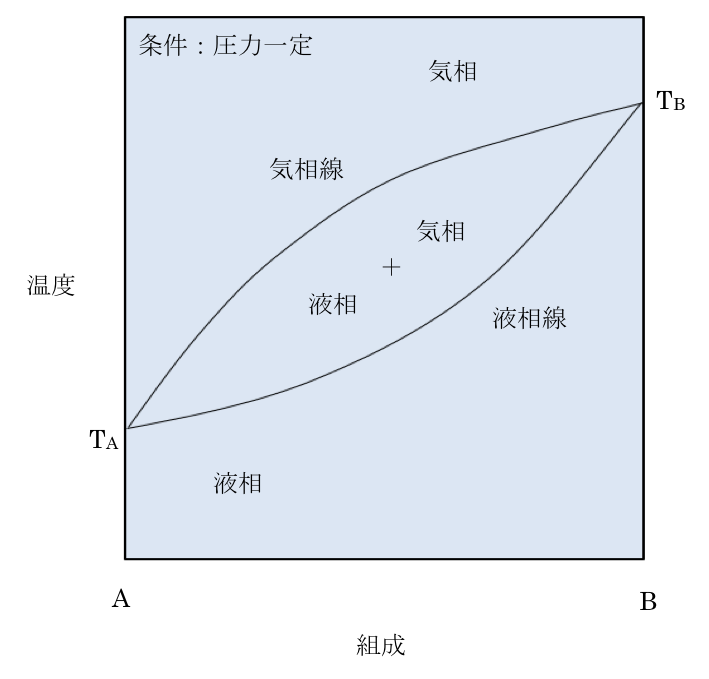
二 成分 系 相 図. 3.3二 成分系状態図 いろいろな集合状態一 気体,液 体,固 体 における,二 つの成分の間の相互作用の大小・正 負によって,多 種多様の状態図が得られる.こ こ では,主 として固体を対象にしているから,(固 体+液体)と(固 体+気体)の 二つの組み合わせ 間の相互作用エネルギー等、成分を系に加え ることによって生じる全てのエネルギー変化 が含まれる. 二成分系の相平衡 水の相図の様一成分系の相図を2つの組成 軸で隔てた2 成分系の相図を右図に示す。こ れを温度一定の面で切るか、圧力一定の面で [4] 相平衡図(3) b 2成分系の相平衡図 <2成分系の相平衡図の読み方> (ii) 系の温度が変化した時の系の状態変化を記述する. 平衡結晶作用(equilibrium crystallization): 平衡溶融作用(fractional crystallization): 分別結晶作用(equilibrium fusion):
ことはそう難しくない。相律の適用例として,氷と水が平衡にある系を考えると,成分は h2oのみであるからc=1, 相は固相(氷)と液相(水)の2つであるからp=2であり,これらを 式(1)に代入すると f=1−2+2=1 (2) となり,変化させることができる示強性変数は1つとなる。これは,たとえ. どの相変態温度は異なるため、例えば2成分系状態図とは fig.3に示すように、 fig.2のl成分系(組成が決まった物質 系)状態図が圧力一定の条件下で組成によって変化する様子 を示していると考えればよい。 く謹)2元系状態図の基本形 機物,有機物などを成分とした二成分系が主であ って,固相と液相の存在領域,変 態の模様などを 組成と温度に対して二次元的に表示した温度一組 成図である.三成分系以上の多成分は複雑なの で,専 門書に譲り,こ こでは扱わない.
単成分系(純物質)で固相の 融解は、融点でのみ起こる。 多成分系(二元系以上)で の固相の融解は、固相線と 液相線で囲まれた温度領域 で起こる。 㱺この領域では固相と液相が平衡 合金の二元系状態図は一般に ・縦軸に温度(℃またはk) ・横軸に組成(wt. 濃度(組成)の単位:mass%(質量%)とwt% (重量%)について 濃度の記述として、si単位の規格や、物理的な解釈として正しいmass%を使うこと が正しい(望ましい)とされているが、世界的にも合金系状態図ではwt%を使用してい ることがほとんどなので、状態図の横軸には本講義でもwt%を用いています。. 相図の背後には必ず自由エネルギーが存在する.一元系の相平衡を自由エネ ルギーから調べてみよう.二つの相を考える.低温で安定なi 相と準安定なii 相(ei 0 < e ii 0) で,異なったばね定数(ki > kii) を持っているとする.先程
3 状態図 1 二成分系の相平衡 二成分系(二つの成分を混合した場合)の相平衡では、相律は、f=c-p+2=2-p+2=4-p と なる。よって、相の数p=1 の場合、f=3 となり、自由度の最大数は3 となる。二成分系では、自由
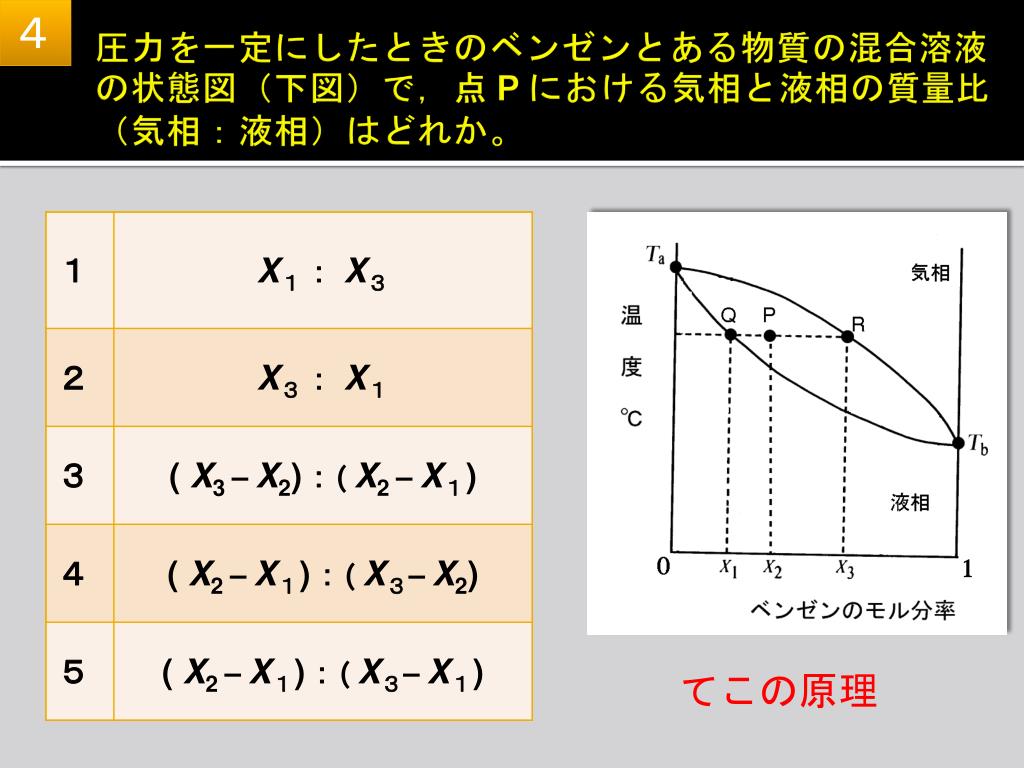
PPT H25 年度 基礎薬学特別講義 I PowerPoint Presentation, free
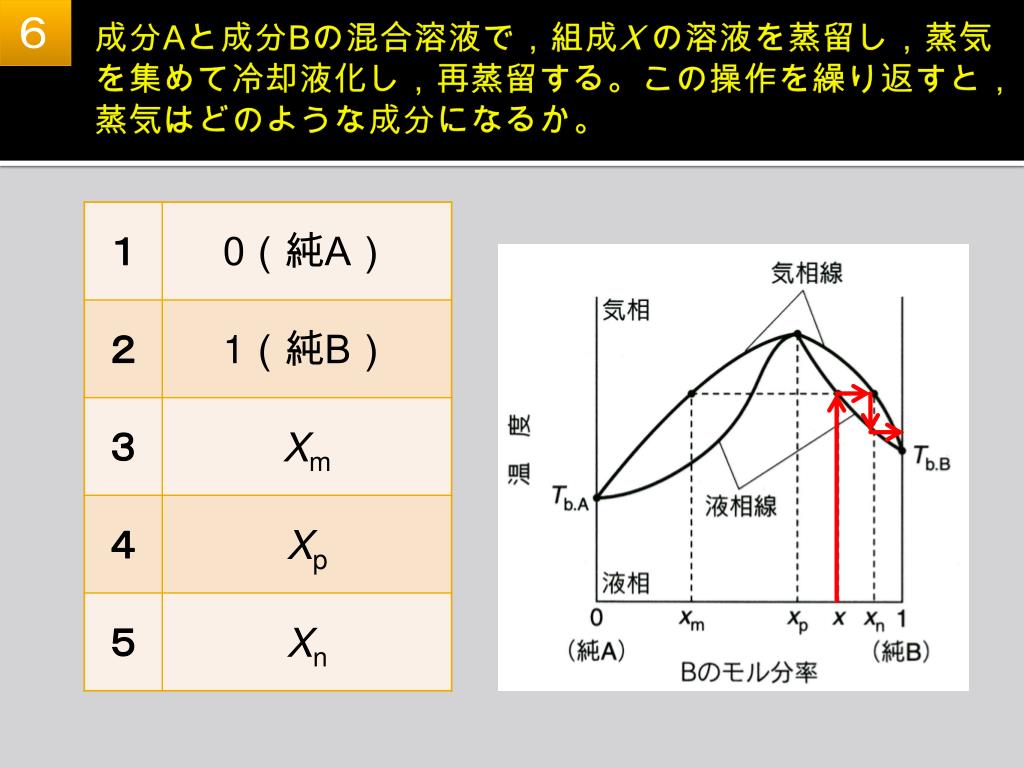
PPT H25 年度 基礎薬学特別講義 I PowerPoint Presentation, free
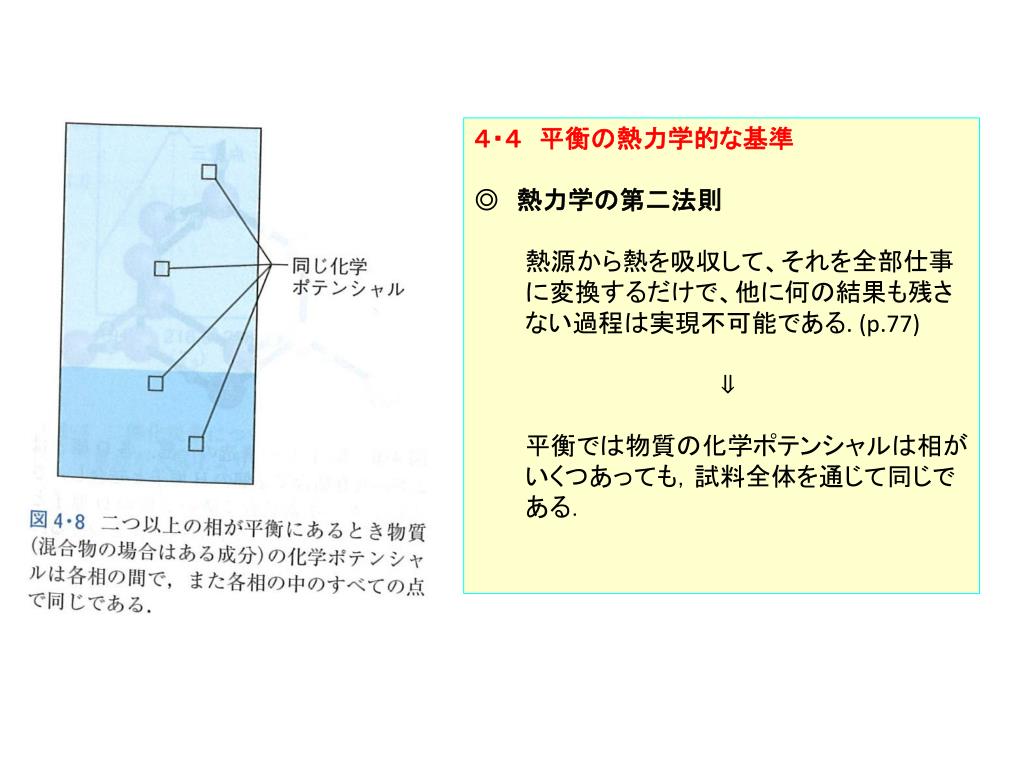
PPT 相の安定性と相転移 相図の特徴を熱力学的考察から説明 以下の考察 物質のギブズエネルギー,とくにその