次のデータについて、四分位数、四分位範囲、四分位偏差を求めなさい。 $$2,3,1,1,5,9,1,4,5$$ まずはデータを大きさの順に並べ替え、中央値を求めましょう。 中央値の値が第2四分位数となります。 中央値の求め方ってどうだっけ…という方はこちらの記事をご参考ください。 参考:中. データを大きさの順に並べたとき、小さい方から 1 4 のところにある数を第1四分位数(q 1)、 大きい方から 1 4 の ところにある数を第3四分位数(q 3)という。第2四分位数(q 2)は中央値である。 データを大きさの順に並べたとき、小さい方.

長岡の教科書_数学1+A【16133N】音声のみ(196頁13行目[3]範囲と四分位偏差—第3回: 箱ひげ図
(2)四分位範囲は第3四分位数から第1四分位数を引いて16-5=11(時間) (3)(1)で求めた四分位数と,最小値2(時間),最大値21(時間) を使って,箱ひげ図をかく。 数学27章データの分布「箱ひげ図」<基本問題②> 組 番 名前 次の2つのデータは,ある中学校の2年生20人のテスト前日の.

四 分 位 範囲 箱 ひげ 図. そして、第一四分位数と第三四分位数の範囲を、四分位範囲(inter quarter range, iqr)と呼んでいます。 箱ひげ図では外れ値も確認できる. 次のデータa,bについて,四分位数,四分位範囲,四分位偏差をそれぞれ求めよ。 a 38,45,47,53,56,57,60,65,69,74,80 b 41,46,54,56,60,63,66,71,75,80 58+62 2. 数学iの「データの分析」の分野には「四分位数 (しぶんいすう) 」という用語が登場します。 これは、下の図のようにデータを小さい順に並べた数の列を、四等分して、四等分した境界に相当するデータ (=3つある) のことです。.
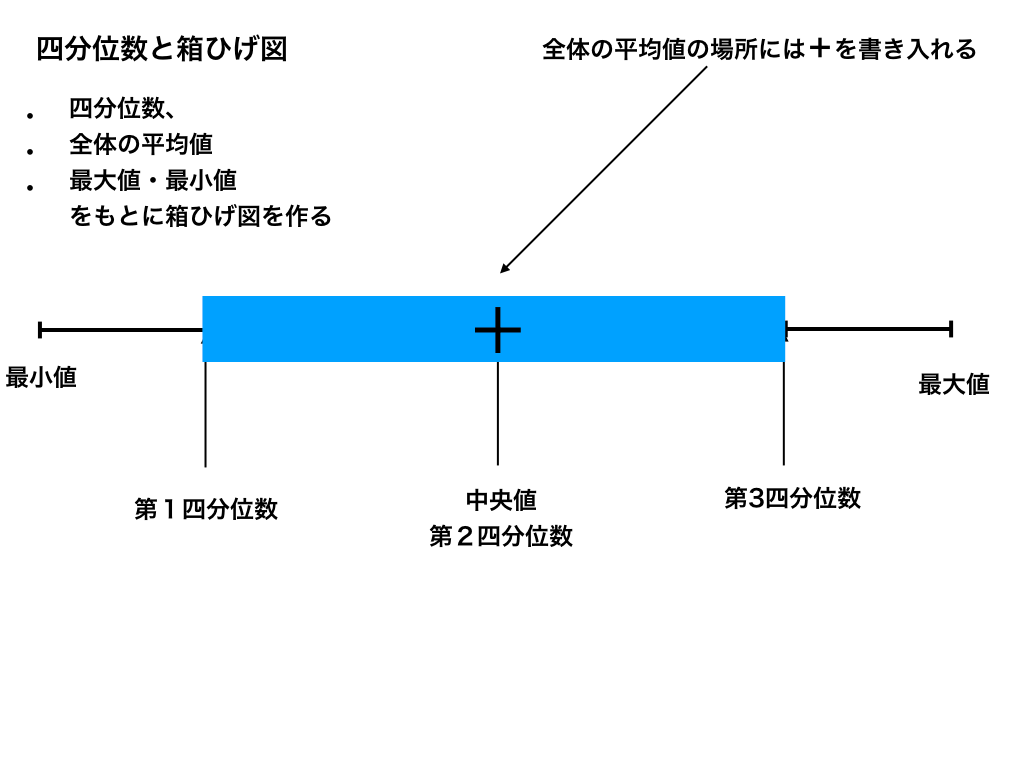
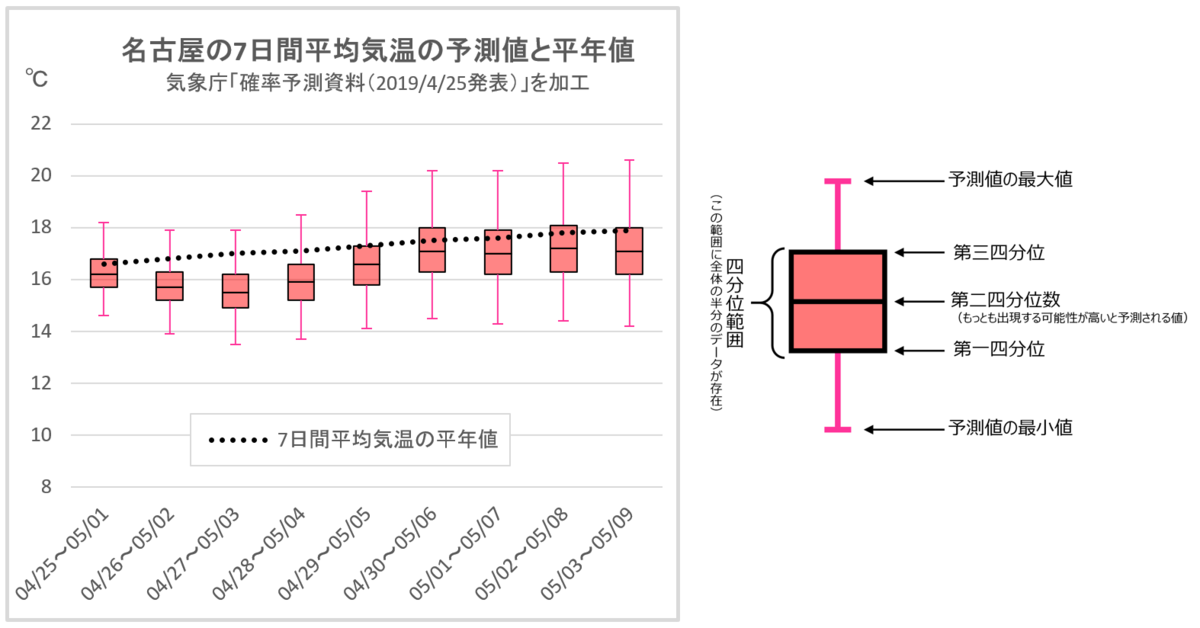
上の項で学んだ第1・第2・第3四分位数と、データの最大・最小値、さらに全データの平均値が用意できれば『箱ひげ図』と呼ばれる図を作成できます。 <箱ひげ図の概要> 上の図のように、 箱 (第1四分位数から第3四分位数の間: 『四部位範囲と呼びます.
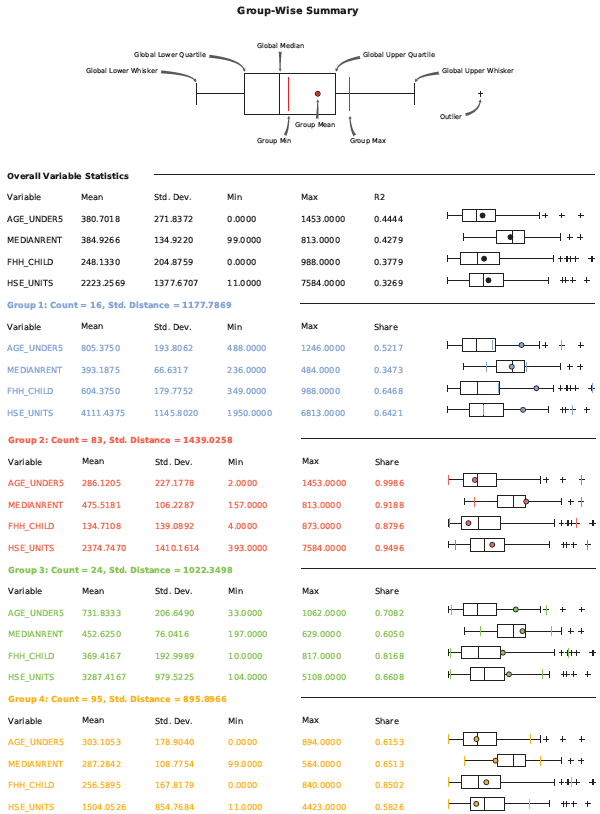
グループ分析 (Grouping Analysis) の詳細—ヘルプ ArcGIS Desktop

【36】Rのggplot2で箱ひげ図を作るgeom_boxplot関数 独学で始める統計×データサイエンス

【高卒認定試験数学】平成29年度2回目 ポイント解説 ページ 2 ひっそりと物理や数学を解説する

【天気コラム】4月20日は二十四節季の「穀雨」。本格的に舞い戻った春、この後どうなる?(2019/4/18) お